부울대수(부울식, 부울식의 법칙, 부울함수, 부울함수의 간소화)

부울대수

0과 1의 조합으로 연산되는 것

전기 장치나 컴퓨터 회로는 켜짐과 꺼짐 두 가지 상태로 나타나기 때문에 부울대수가 필요하다.

부울식

두 원소를 가지는 집합 A＝{0, 1}와 이항 연산자(binary operator) ＋(OR)과 ∙ (AND), 그리고 단항 연산자(unary operator) ′(complement)로 표현되는 식을 말함

부울식에서 연산자의 연산 우선순위는 ′(NOT) > ⋅(AND)  >＋(OR) 순

 

위와 같이 0과 1로만 표현되고 논리연산자는 똑같이 적용하고 있음을 알 수 있다.

+는 OR, ∙은 AND연산자임을 헷갈리지 말자

 

부울식은

1. 상수 0과 1 , 부울 변수는 부울식이다.

2. f₁과 f₂가 부울 식일때, 이를 논리연산자로 계산하는 식 또한 모두 부울식이라고 할 수 있다.

 

부울식에서 부울 변수 x, y, z가 가질 수 있는 값인 0 또는 1을 정해줌으로써 각 부울식에 대한 값을 구할 수 있다.

두 부울식이 같은 진리표(truth table)를 가질 경우 두 부울식을 동치(equivalent)라 하고

두 함수 f₁과 f₂가 동치인 경우 f₁＝f₂로 표시한다.

 

부울식의 법칙

집합과 더불어 드모르간의 법칙은 여기서도 쓰인다. 중요하니 외워둘 것.

 

부울 함수

부울 변수들에 대한 함수를 부울 함수(Boolean function이라 하고 n개의 부울 변수 x1, x2, …, xn에 대한 부울 함수는  f (x1, x2, …, xn)으로 표시한다.

괄호 안에는 해당 함수에 들어가는 변수들을 쓰고 우항은 함수를 쓰면 된다.

부울함수는 부울 변수와 부울 연산자로 구성된 부울식으로 표현할 수 있다.

n개의 부울 변수가 있을 때 그 변수들로부터 얻을 수 있는 조합은 00…0, 00…1, …, 11…1로 2의 n승 개이다. 비트의 수라고 생각하면 개수를 왜 이렇게 계산하는지 알 수 있다.

참고로 0은 그에 해당되는 원소가 없는 경우이고, 1은 있는 경우로 생각한다.

이 n개의 부울 변수로 만들어지는 진리표에서 변수의 각 항을 최소항(Minterm)이라 하며, 그냥 나올 수 있는 조합들이라고 생각하면 된다.



해당 부울함수는 x=1, y=0, z=1일 때 1이 되는 함수이다.

여기서 최소항은 7개인 0과 1개인 1로 총 8개인 셈. 2의 3승개이므로 2의 (변수개수)승이라고 볼 수 있다.

해당 함수를 구할 때는 1이 만들어 지는 경우가 하나밖에 없다.

x=1, y=0, z=1일때 뿐이기 때문에

f(x,y,z) = xy'z가 된다

'는 NOT을 의미함으로 1의 보수는 0이기 때문에 0을 표현할 때는 '를 붙이고 1을 표현할 때는 그냥 변수만 쓴다.

다시 한번 함수를 구해보면

해당 함수는 1일때의 값이 세 개가 있다.

1. x=0, y=0, z=1일 때

2. x=1, y=0, z=0일 때

3. x=1, y=1, z=0일 때

이 세개가 있으므로 해당 조건마다 모두 변수의 조건을 만족시켜야 하기 때문에 논리곱으로 묶고 논리합으로 더한다.

따라서

f(x,y,z) = x'y'z + xy'z' + xyz'가 되는 것이다.

 

부울식의 곱의 합 표현

곱의 합(sum of products) 또는 논리합 표준형(Disjunctive Normal Form : DNF)은 부울 함수를 나타내는 데 있어서 최소항들의 합으로 표현하는 것이다.

최소항들은 부울 변수의 곱으로 표현되고, 부울 함수는 부울 변수의 곱의 합으로 표현된다.

별건 없고 위에처럼 표시하면 된다.

 

부울 함수의 간소화

부울 변수의 최소항들로부터 얻어진 부울 함수는 좀 더 간단한 형태의 식으로 만들 수 있다.

간소한 형태의 식이란 같은 기능이나 결과를 도출하면서도 더 적은 변수와 연산자를 사용한 식이다.

생략할만한 변수와 연산자를 생략하는 것이다.

하지만 이는 확실한 때만 생략이 가능하므로 주의해서 써야 한다.

부울함수식을 간소화시키는 방법은 두 가지가 있다.

1. 부울식의 기본 법칙 사용

위에 나온 부울식의 기본 법칙을 사용해서 간소화를 시킬 수 있다.

하지만 양이 많아지면 많아질수록 이를 하나하나 분리해서 뭐와 조합하여 생략시키고 하면 과정이 복잡해진다는 단점이 있다.

이런 식으로 쓰는건데, 법칙을 여러번 쓰는게 피곤하고 복잡해서 주로 카노우맵을 쓴다.

2. 카노우맵을 사용

카노우맵은 부울 변수에 대한 최소항들을 도표로 그린 것이다.

인접한 최소항끼리 묶어서 표현하면 어떤 변수를 생략할 수 있는지 쉽게 알 수 있다.

 

카노우맵을 그릴 때는 부울 변수들로부터 나타내어지는 모든 경우의 최소항들을 사각형으로 연결시켜서, 최소항들 중 1의 값을 가지는 사각형 안에‘1’을 표시한다.

이런 식으로 해당 변수들에 해당하는 값을 넣어 표시하는 것이다.

0또한 쓸 수도 있지만, 어차피 0은 최소항이 1을 가진 값만 함수식에 포함시키니 따로 쓸 필요가 없다.

 

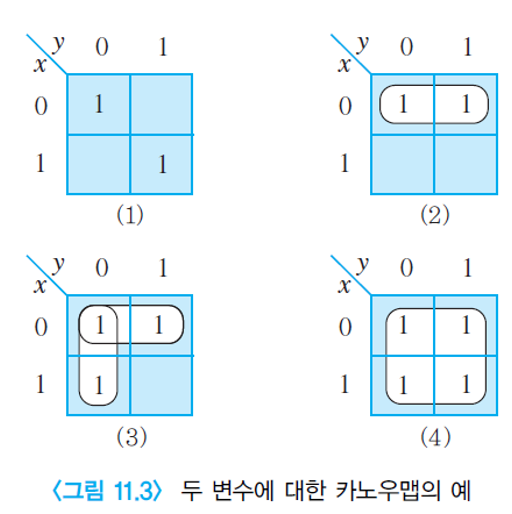
‘1’로 표시된 사각형들에서 부울식의 공통점을 찾아내어 부울 함수를 간소화시킨다.

사각형을 연결시킬 때는 인접한 사각형끼리는 한 변수의 변화만 있게 만들어야 한다.

따라서 바로 옆집들만 가능하다.

(1)의 경우에는 서로 인접한 1이 없어 묶을 수가 없으므로 각각 따로 표현하면 x’y’＋ xy가 됨

(2) y의 값이 0이든 1이든 관계없이 x의 값이 0 일 때, 다시 말해 x’일 때 1의 값을 가지므로 x’가 됨

(3) 윗부분의 묶음은 (2)의 경우와 같고, 아래쪽으로의 묶음은 x의 값에 관계없이 y’이므로, 부울식은  x’ ＋ y’가 됨

 

(4) x와 y의 값에 관계없이 항상 1이므로 부울식은 1이 됨

 

따라서 무조건 바뀌지 않는 고정된 변수는 포함시키고, 0과 1 모두 포함되는 변수는 생략가능한 것이다.

세 변수에 대한 카노우맵도 한 옆에는 두 가지 변수의 조합을 넣어놓아 4*2의 형태로 만들 수 있다.

주의할 점은 yz에 대한 사각형에서 오른쪽 방향으로 00, 01 다음에 10이 아니라 11이 먼저이다.

두 변수가 한꺼번에 변하는 것은 인접할 수가 없기 때문에 01 옆에는 10이 아닌 11이 오는 것.

왼쪽 끝의 사각형들은 오른쪽 끝의 사각형들과 인접되어 있다고 생각해야 함. 그냥 동그랗게 말아서 붙여놓는다고 생각하면 편하다. 양 끝을 붙여놓으면 z의 값은 같고 y의 값만 다른 것을 알 수 있다.

따라서 두 변수가 한번에 변하지 않기 때문에 인접한 것으로 생각할 수 있다.

해당 진리표를 카노우맵으로 표현해보면 

이런 모양으로 나온다

보면 x'yz가 겹쳐져 있는 것을 알 수 있다.

하지만 겹치지 않으면 x'y를 표현할 방법이 없기 때문에 겹쳐 쓰는 것이다.

그러므로 한 가지 최소항만 남았을 때는 겹쳐 쓰지만, 모두 나눠지면 따로 겹쳐 새로운 것을 만들 필요가 없다.

네 변수에 대한 카노우맵도 2개 변수씩 넣어서 쓰므로 해당 00 01 11 10순으로 행과 열을 쓰면 된다.

왼쪽 끝 사각형들과 오른쪽 끝 사각형들이 인접하고 있다고 보며, 위쪽 사각형들과 아래쪽 사각형들 역시 인접하고 있다고 본다.

아까와 같이 동그랗게 말아서 붙여보면 알 수 있다.